Logo
目录
Back to the blog→
Previous:Unity 制作萌系live2d桌宠：屏幕自适应+交互Next:Phoenix Introduce
Published on

一份代码四个算法：广度优先BFS、Dijstra、最佳优先BFS、A*

一份代码四个算法：广度优先BFS、Dijstra、最佳优先BFS、A*

Authors

Authors
  • avatar
    Name
    Astar
    Twitter
    @bilibili
    广度优先BFS、Dijstra、最佳优先BFS、A*四个最短路径算法简明解析，最后发现他们就像一个算法

目录

转自本人csdn

三种比较经典的最短路径算法Dijkstra、最佳优先、A*，他们本质上都由广度优先扩展而来，其实掌握广度优先算法也就掌握了这些寻路算法。

"游戏"的地图

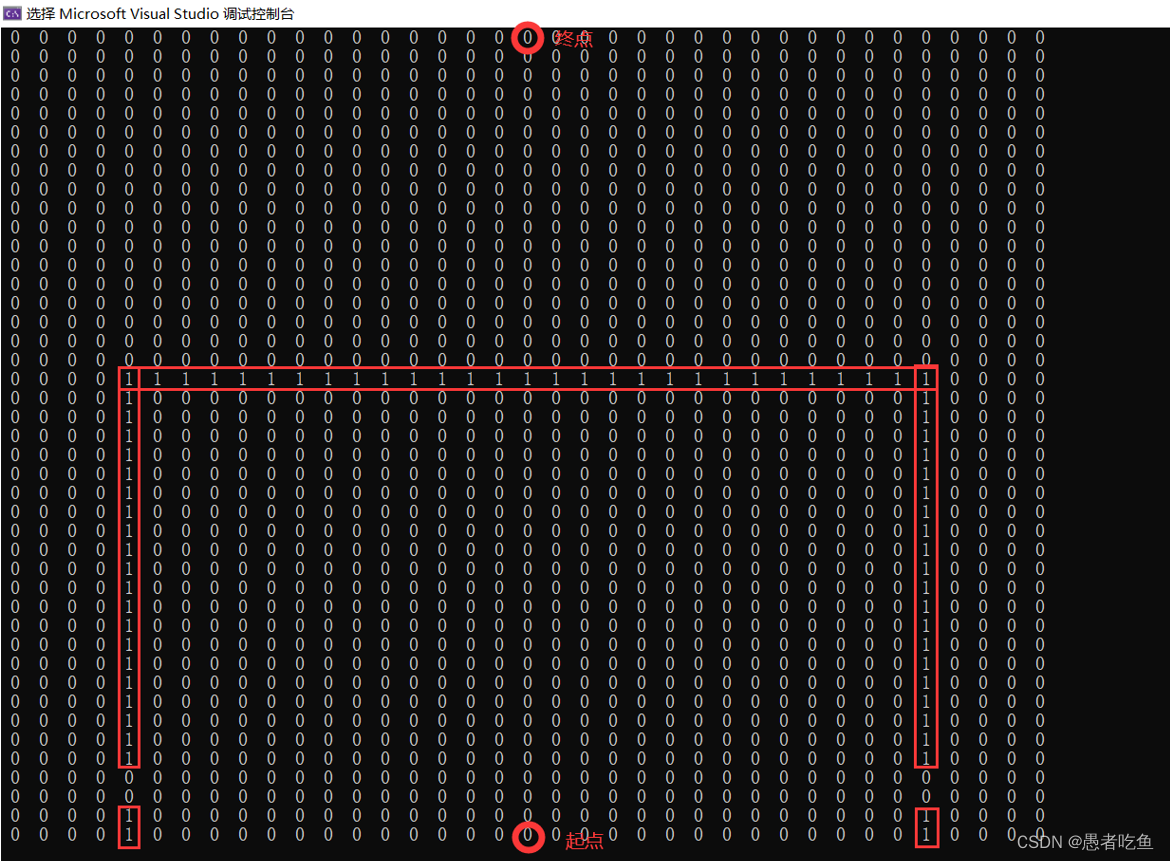
寻路算法必须有地图，这里使用只包含0、1的矩阵表示游戏地图。 其中，“1”表示墙（不可访问），“0”表示可访问但尚未访问的地方

在这里插入图片描述

代码

//最短路径算法C++
const int map_width = 37; //地图宽度
const int map_height = 43; //地图高度
//相关数组
vector<vector<int>> game_map(map_height, vector<int>(map_width));//地图
game_map = {
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},		
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},		
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},		
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},
	{0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0}
};

一切的起点——广度优先

广度优先是最简单的寻路算法，也是本文剩余算法的基础，其本质是使用一个队列，按照移动的次数递增的顺寻遍历全图。 代码

//辅助内容
//移动方向以及代价
int add_x[8] = { -1,1,0,0,-1,-1,1,1 };
int add_y[8] = { 0,0,-1,1,-1,1,-1,1 };
double add_c[8] = { 1,1,1,1,1.414,1.414,1.414,1.414 };//代价
//辅助节点
struct node {
	int x;
	int y;
	double total_cost;//广度优先用不到
	double path_cost;//广度优先、Dijstra、最佳优先用不到
};
node begin = { map_height-1,map_width/2,0,0 };//起始节点
node target = { 0,map_width/2,0,0 };//目标节点
//打印函数
void print_map(vector<vector<int>>& game_map, vector<vector<double>>& gone_node, vector<vector<int>>& last_node, node& begin, node& target) {
	//打印走的路径
	game_map[begin.x][begin.y] = 2;
	game_map[target.x][target.y] = 2;
	int last = last_node[target.x][target.y];
	while (last != -1) {
		game_map[last / map_width][last % map_width] = 2;
		last = last_node[last / map_width][last % map_width];
	}
	for (int i = 0; i < map_height; ++i) {
		for (int j = 0; j < map_width; ++j) {
			if (game_map[i][j] == 2)cout << " G ";
			else if (gone_node[i][j] == DBL_MAX)cout << " 0 ";
			else if (game_map[i][j] == 1)cout << " 1 ";
			else cout << " * ";
		}
		cout << endl;
	}
}
//广度优先
bool bfs(vector<vector<int>>& game_map,node& begin, node& target) {
	queue<node> qu;//目前可去节点
	vector<vector<double>> gone_node(map_height, vector<double>(map_width, DBL_MAX));//到达过的节点
	vector<vector<int>> last_node(map_height, vector<int>(map_width,-1));//到达此节点的上一个节点
	qu.push(begin);
	//标记起点已经走过
	gone_node[begin.x][begin.y] = 1;
	while (!qu.empty()) {
		node current = qu.front();
		qu.pop();
		//走到目标直接返回true
		if (current.x == target.x && current.y == target.y) {
			print_map(game_map,gone_node,last_node,begin,target);
			return true;
		}
		//将八个方向的坐标插入队列
		for (int i = 0; i < 8; ++i) {
			int xx = current.x + add_x[i];
			int yy = current.y + add_y[i];
			if (xx < 0 ||//走到边界的情况直接略过
				xx >= map_height ||
				yy < 0 ||
				yy >= map_width || 
				game_map[xx][yy] == 1||//到墙前面的情况直接略过
				gone_node[xx][yy] == 1//走过的节点直接略过
				)continue;
			qu.push({ xx,yy });
			gone_node[xx][yy] = 1;//标记当前的路已经走过
			last_node[xx][yy] = current.x * map_width + current.y;
		}
	}
	return false;
}
在这里插入图片描述

地图中元素的含义：

  • 0：墙或者没走过的节点
  • *：广度优先算法探索过的地方
  • G：最终的路径

分析： 可以发现，广度优先得到的结果是最优的，这是为什么呢？ 实际上，在当前地图上广度优先和Dijstra效果是一样的，原因下面解释。

Dijstra算法

非常经典的算法，其本质是在广度优先基础上，以已经走过的距离为标准，以一定顺序遍历全图。

对于广度优先来说，遍历某个节点的时候，需要把与它相连的节点全部送入队列末尾，而Dijstra不同，节点在队列中的顺序是按照其已经走过的距离排列的。

也就是说，把广度优先中的队列改成按照已经走过的距离排序的优先级队列就ok了。

于是，Dijstra算法便呼之欲出了

代码

//与广度优先使用相同的辅助内容、移动方向以及代价、辅助节点和打印函数

//用于C++优先级队列中元素的比较
class Compare {
public:
	bool operator()(node& left, node& right) {
		return left.total_cost > right.total_cost;
	}
};
//Dijkstra
bool dijkstra(vector<vector<int>>& game_map,node& begin, node& target) {
	priority_queue<node,vector<node>, Compare> qu;//目前可去节点  ①换成了优先级队列
	vector<vector<double>> gone_node(map_height, vector<double>(map_width, DBL_MAX));//到达过的节点
	vector<vector<int>> last_node(map_height, vector<int>(map_width, -1));//到达此节点的上一个节点
	qu.push(begin);
	//标记起点已经走过
	gone_node[begin.x][begin.y] = 1;
	while (!qu.empty()) {
		node current = qu.top();
		qu.pop();
		//走到目标直接返回true
		if (current.x == target.x && current.y == target.y) {
			print_map(game_map, gone_node, last_node, begin, target);
			return true;
		}
		//将八个方向的坐标插入队列
		for (int i = 0; i < 8; ++i) {
			int xx = current.x + add_x[i];
			int yy = current.y + add_y[i];
			/*走到边界的情况直接略过
			* 走到墙前面的情况直接略过
			* 走回头路（刚刚走过的路）的情况直接略过
			*/
			double cost = current.total_cost + add_c[i];  //②需要计算已经走过的距离
			if (xx < 0 ||//走到边界的情况直接略过
				xx >= map_height ||
				yy < 0 ||
				yy >= map_width ||
				game_map[xx][yy] == 1 ||//到墙前面的情况直接略过
				gone_node[xx][yy] == 1//走过的节点直接略过
				)continue;
			qu.push({ xx,yy,cost });//③插入队列的时候加上已经走过的距离
			//标记当前的路已经走过
			gone_node[xx][yy] = 1;
			last_node[xx][yy] = current.x * map_width + current.y;
		}
	}
	return false;
}

抛开新定义的Compare ，只改动了三处，便从广度优先转变成Dijstra算法了。

在这里插入图片描述

解释 对于地图上的四个点：

A B C D

由前面代码可知AB、AC、DC...之间的距离是1，AD和CB之间的记录是1.414。

  • 对于Dijstra：距离派上了用处，AB、AC、DC…之间的距离是1，AD和CB之间的记录是1.414，因此Dijstra的结果是包含最少移动距离的路径。
  • 对于广度优先：距离是用不上的，ABCD任意两个点之间的距离都视作1，因此广度优先的结果是包含最少移动次数的路径。
  • 不难发现，在上述地图上，对于两种算法，走对角（从A到D，走一个节点）代价总是比走拐角（从A到B再到D，走两个姐点）的代价低，所以他们的结果一致。真实的地图上，多个节点连成的路也许比两个节点直连的路代价更小，这时才能体现出Dijstra以及其他寻路算法的优越性。

最佳优先算法BFS

最佳优先（Best First Search）缩写也叫BFS，而它与广度优先也很相似，其本质是在广度优先基础上，以启发式估算的距离为标准，以一定顺序遍历全图。

启发式又称估价函数，它的作用是对将要遍历的节点进行估价，在本文中，我们使用欧几里得距离进行估价。

好了，上代码

代码

//与Dijstra使用相同的辅助内容、移动方向以及代价、辅助节点和打印函数、Compare类

bool bestfirst(vector<vector<int>>& game_map, node& begin, node& target) {
	priority_queue<node, vector<node>, Compare> qu;//目前可去节点
	vector<vector<double>> gone_node(map_height, vector<double>(map_width, DBL_MAX));//到达过的节点
	vector<vector<int>> last_node(map_height, vector<int>(map_width, -1));//到达此节点的上一个节点
	qu.push(begin);
	gone_node[begin.x][begin.y] = begin.total_cost;	//①初始代价
	while (!qu.empty()) {
		node current = qu.top();
		qu.pop();
		//走到目标直接返回true
		if (current.x == target.x && current.y == target.y) {
			print_map(game_map, gone_node, last_node, begin, target);
			return true;
		}
		//将八个方向的坐标插入队列
		for (int i = 0; i < 8; ++i) {
			int xx = current.x + add_x[i];
			int yy = current.y + add_y[i];
			double cost = sqrt(pow((double)xx - target.x, 2) + pow((double)yy - target.y, 2));//② 计算启发式
			if (xx < 0 ||//走到边界的情况直接略过
				xx >= map_height ||
				yy < 0 ||
				yy >= map_width ||
				game_map[xx][yy] == 1 ||//到墙前面的情况直接略过
				gone_node[xx][yy] <= cost//③当前路径代价更小才走 
				)continue;
			qu.push({ xx,yy,cost });
			gone_node[xx][yy] = cost;//④更新节点代价
			last_node[xx][yy] = current.x * map_width + current.y;
		}
	}
	return false;
}

相对于Dijstra，改动了四处，Dijstra保证每一步找出的节点都是距离最优的，而最佳优先没有这个保证，它甚至不一定能找出最优路线......

在这里插入图片描述
  • 0：墙或者没走过的节点
  • *：广度优先算法探索过的地方
  • G：最终的路径

可以发现，最佳优先经过的无关节点更少了，找到单条路径效率更高了，然而该路径并不是最优的（事实上，寻找一个节点到其他所有节点的最短路径还得看Dijstra）

A*

最后是A*算法，它把Dijstra算法和最佳优先算法结合到了一起，在广度优先的基础上，同时考虑已经走过的距离和启发式函数，以一定顺序遍历全图。

代码

//与Dijstra使用相同的辅助内容、移动方向以及代价、辅助节点和打印函数、Compare类

//A*
bool AStar(vector<vector<int>>& game_map, node& begin, node& target) {
	priority_queue<node, vector<node>, Compare> qu;//目前可去节点
	vector<vector<double>> gone_node(map_height, vector<double>(map_width, DBL_MAX));//到达过的节点
	vector<vector<int>> last_node(map_height, vector<int>(map_width, -1));//到达此节点的上一个节点
	qu.push(begin);
	//标记起点已经走过
	gone_node[begin.x][begin.y] = 0;
	while (!qu.empty()) {
		node current = qu.top();
		qu.pop();
		//走到目标直接返回true
		if (current.x == target.x && current.y == target.y) {
			print_map(game_map, gone_node, last_node, begin, target);
			return true;
		}
		//将八个方向的坐标插入队列
		for (int i = 0; i < 8; ++i) {
			int xx = current.x + add_x[i];
			int yy = current.y + add_y[i];
			double cost = sqrt(pow((double)xx - target.x, 2) + pow((double)yy - target.y, 2)) + current.path_cost+add_c[i];//①同时考虑已经走过的距离和启发式函数
			if (xx < 0 ||//走到边界的情况直接略过
				xx >= map_height ||
				yy < 0 ||
				yy >= map_width ||
				game_map[xx][yy] == 1 ||//到墙前面的情况直接略过
				gone_node[xx][yy] <= cost//当前路径代价更小才走
				)continue;
			qu.push({ xx,yy,cost, current.path_cost + add_c[i] });
			//标记当前的路已经走过
			gone_node[xx][yy] = cost;
			last_node[xx][yy] = current.x * map_width + current.y;
		}
	}
	return false;
}

相对于最佳优先算法只改了一处......

在这里插入图片描述

从结果上来看，确实综合了Dijstra的好处和最佳优先的好处。

Discuss on Twitter • View on GitHub←Back to the blog